17 25 As A Percent
marihuanalabs
Sep 07, 2025 · 5 min read
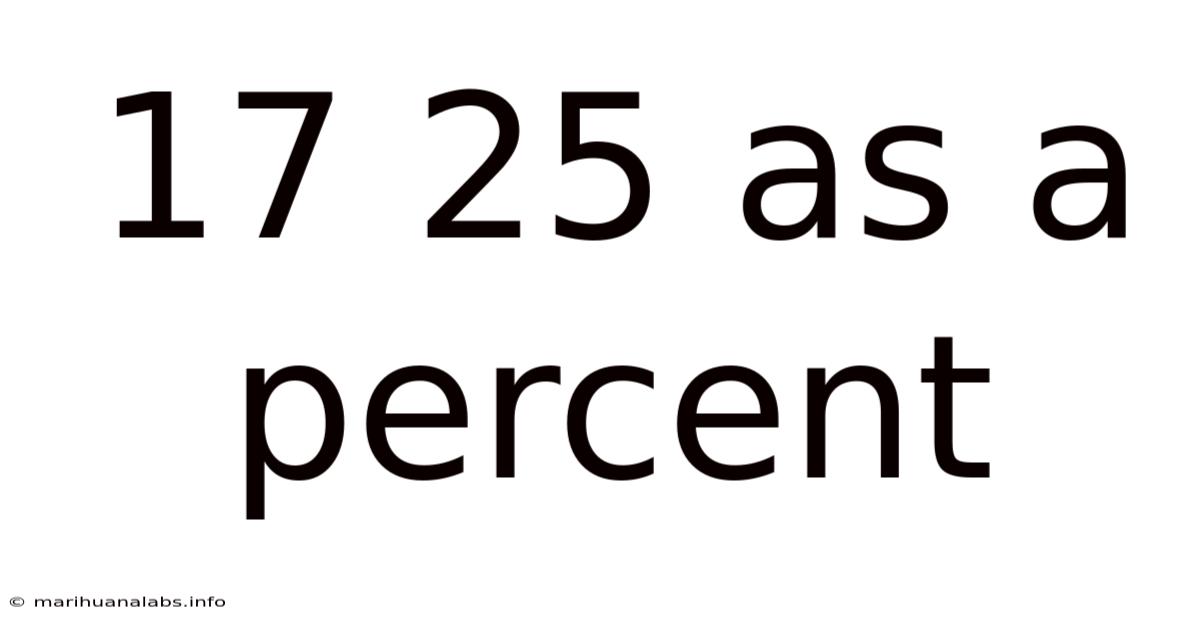
Table of Contents
17 out of 25 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with applications spanning various fields, from everyday finances to advanced scientific calculations. This article provides a comprehensive guide on calculating and interpreting "17 out of 25 as a percentage," exploring different methods, clarifying common misconceptions, and offering practical applications to solidify your understanding. We'll delve into the process step-by-step, making it easy for anyone, regardless of their mathematical background, to grasp the concept fully.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are used extensively to represent proportions, ratios, and changes in value. Calculating "17 out of 25 as a percentage" involves determining what fraction of 100 17 represents when compared to 25.
Method 1: Using the Fraction Method
The most straightforward approach is to convert the given ratio into a fraction and then convert that fraction into a percentage.
-
Express as a Fraction: "17 out of 25" can be written as the fraction 17/25.
-
Convert to a Decimal: Divide the numerator (17) by the denominator (25): 17 ÷ 25 = 0.68
-
Convert to a Percentage: Multiply the decimal by 100: 0.68 x 100 = 68%
Therefore, 17 out of 25 is equal to 68%.
Method 2: Using Proportions
This method uses the concept of proportions to solve the problem. We set up a proportion where 'x' represents the percentage we want to find:
17/25 = x/100
To solve for 'x', we cross-multiply:
25x = 1700
Then, divide both sides by 25:
x = 1700 ÷ 25 = 68
Therefore, x = 68%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 17 ÷ 25 and then multiply the result by 100. The calculator will directly display the answer as 68%. This is the quickest method, particularly useful for more complex calculations.
Understanding the Result: 68%
The result, 68%, means that 17 represents 68 out of every 100 parts of the whole (25). This percentage can be interpreted in various contexts depending on the scenario. For example, if 17 out of 25 students passed an exam, it means 68% of the students were successful.
Practical Applications of Percentage Calculations
Understanding percentages is crucial in various real-world situations:
-
Financial Calculations: Calculating interest rates, discounts, taxes, and profit margins all involve percentages. For instance, a 10% discount on a $100 item means a saving of $10.
-
Data Analysis and Interpretation: Percentages are frequently used to represent data in graphs, charts, and reports. This allows for easy comparison and visualization of proportions within datasets. For example, understanding market share percentages helps businesses analyze their performance relative to competitors.
-
Academic Performance: Grades are often expressed as percentages, providing a clear indication of student performance. A score of 68% on a test, for example, shows a relatively good understanding of the material.
-
Scientific Research: Percentages are employed to represent statistical data, helping researchers draw conclusions and analyze results from experiments or surveys.
-
Everyday Life: We encounter percentages daily, from sales promotions to nutritional information on food labels. Understanding percentages empowers us to make informed decisions in various aspects of our daily lives.
Common Misconceptions about Percentages
Several common misconceptions surround percentages, leading to errors in calculations and interpretations.
-
Confusing Percentage with Absolute Value: A 10% increase in a large value will be significantly greater than a 10% increase in a small value. It's crucial to consider the absolute values alongside the percentage change.
-
Incorrectly Calculating Percentage Change: When calculating a percentage increase or decrease, the base value must be correctly identified. For example, to calculate the percentage increase from 20 to 25, the base value is 20. The increase is 5, and the percentage increase is (5/20) * 100 = 25%.
-
Misinterpreting Percentages in Contexts: The context of the percentage is critical. A 68% success rate on a test might be considered good, but a 68% success rate in a life-saving surgery might be alarming.
Advanced Concepts related to Percentages
While calculating "17 out of 25 as a percentage" is a basic application, understanding more advanced concepts enhances your mathematical skills:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100.
-
Percentage Points: This refers to the arithmetic difference between two percentages. For example, an increase from 20% to 25% is a 5 percentage point increase, not a 25% increase.
-
Compounding Percentages: This applies when percentages are applied successively. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Weighted Averages: This involves calculating the average of a set of values, each weighted by its corresponding percentage.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase?
- A: Use the formula: [(New Value - Old Value) / Old Value] x 100
-
Q: How do I calculate a percentage decrease?
- A: Use the formula: [(Old Value - New Value) / Old Value] x 100
-
Q: What is the difference between percentage and percentage points?
- A: Percentage points represent the absolute difference between two percentages, while percentages represent a proportional change.
-
Q: Can I use a calculator to calculate percentages?
- A: Yes, most calculators have a percentage function that simplifies the calculation.
-
Q: What if I have a fraction that's not easily converted to a decimal?
- A: You can use long division to convert the fraction to a decimal, then multiply by 100 to get the percentage.
Conclusion: Mastering Percentage Calculations
This article provided a comprehensive guide to calculating "17 out of 25 as a percentage," demonstrating different methods and highlighting practical applications. Mastering percentage calculations is essential for various aspects of life, from personal finance to professional endeavors. By understanding the underlying principles and avoiding common misconceptions, you can confidently tackle percentage problems and utilize this fundamental mathematical skill effectively. Remember that practice is key to mastering any mathematical concept. Work through various examples, and don't hesitate to seek further resources if needed. With consistent effort, you will develop a strong understanding of percentages and their wide-ranging applications.
Latest Posts
Latest Posts
-
Its A Far Better Thing
Sep 08, 2025
-
Jack And The Beanstalk Book
Sep 08, 2025
-
The Pixies Que Sera Sera
Sep 08, 2025
-
Map Of The Maginot Line
Sep 08, 2025
-
Would You Like In French
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 17 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.