11 15 As A Percentage
marihuanalabs
Sep 20, 2025 · 5 min read
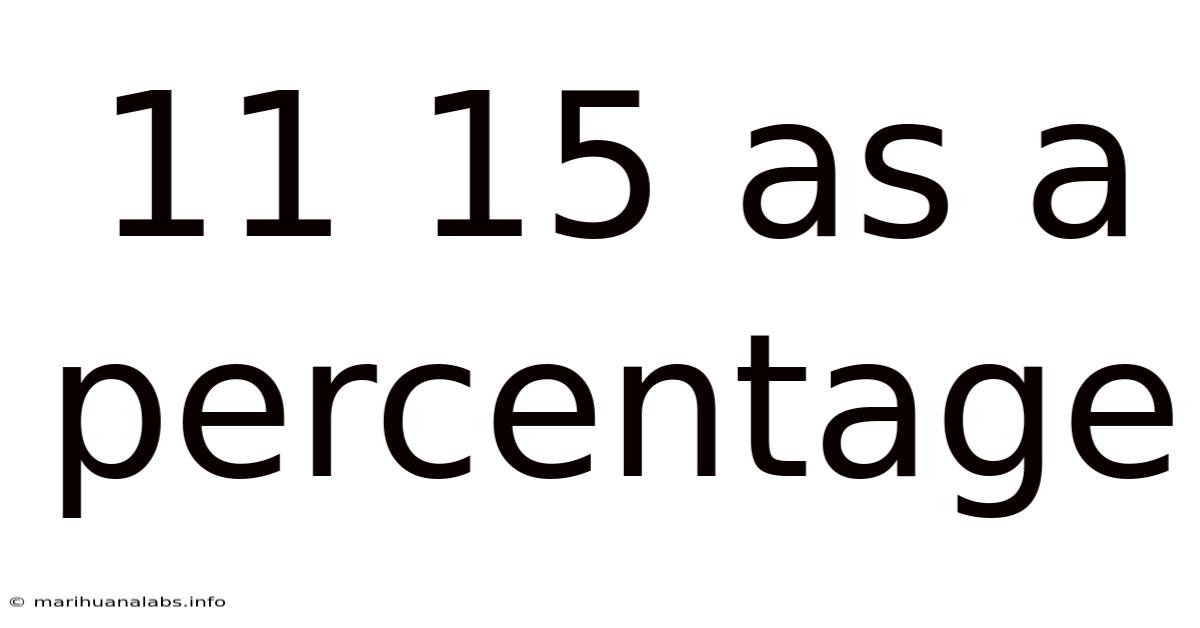
Table of Contents
Understanding 11/15 as a Percentage: A Comprehensive Guide
Knowing how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a store to understanding statistical data. This article provides a thorough explanation of how to convert the fraction 11/15 into a percentage, along with different methods and valuable insights into the underlying mathematical concepts. We’ll cover various approaches, explore the significance of percentages, and address frequently asked questions to build a solid understanding of this essential concept.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. In the fraction 11/15, 11 is the numerator (the part) and 15 is the denominator (the whole). A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage is through division. We divide the numerator by the denominator and then multiply the result by 100.
Here's how to do it for 11/15:
-
Divide the numerator by the denominator: 11 ÷ 15 ≈ 0.7333
-
Multiply the result by 100: 0.7333 × 100 = 73.33
Therefore, 11/15 is approximately 73.33%. The "≈" symbol indicates that this is an approximation because the decimal representation of 11/15 is non-terminating (it goes on forever). We typically round to two decimal places for percentage calculations unless higher precision is required.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction with a denominator of 100. This method relies on the principle of equivalent fractions, which states that multiplying or dividing both the numerator and denominator of a fraction by the same non-zero number does not change its value.
Since we want a denominator of 100, we need to find a number that, when multiplied by 15, gives 100. However, 100 is not perfectly divisible by 15. Instead, we can use a different approach:
-
Set up a proportion: We can set up a proportion to solve this: 11/15 = x/100
-
Cross-multiply: 15x = 1100
-
Solve for x: x = 1100/15 ≈ 73.33
Therefore, 11/15 is approximately equivalent to 73.33/100, which is 73.33%. This method demonstrates the underlying relationship between fractions and percentages.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the conversion process. Simply enter 11 ÷ 15 and then multiply the result by 100. This method offers efficiency and eliminates the possibility of manual calculation errors. The calculator will directly display the percentage, typically with the appropriate rounding.
Understanding the Significance of Percentages
Percentages are a crucial tool for expressing proportions and comparisons in various contexts:
- Business and Finance: Calculating profit margins, interest rates, discounts, tax rates, and investment returns.
- Science: Representing experimental data, statistical probabilities, and compositional analysis.
- Everyday Life: Understanding sales, tips, inflation rates, and survey results.
- Education: Grading systems, performance assessments, and statistical analysis of educational data.
Mastering percentage calculations allows for a more profound understanding of data and improved decision-making in numerous aspects of life.
Illustrative Examples
Let's consider some real-world scenarios where understanding 11/15 as a percentage is relevant:
-
Test Scores: If a student answered 11 out of 15 questions correctly on a test, their score would be 73.33%. This allows for easy comparison with other students and provides a clear picture of their performance.
-
Sales Discounts: A store offering a 11/15 discount on an item implies a discount of approximately 73.33%. This is essential for customers to easily understand the price reduction.
-
Survey Results: If 11 out of 15 respondents favor a particular policy, the percentage in favor is approximately 73.33%. This helps in analyzing public opinion and making informed decisions.
Further Exploration: Working with Percentages
Understanding how to convert fractions like 11/15 to percentages is a foundational step. Building on this, you can explore more advanced concepts such as:
- Percentage Increase/Decrease: Calculating the percentage change between two values.
- Finding a Percentage of a Number: Determining a specific percentage of a given quantity.
- Converting Percentages to Fractions and Decimals: Understanding the interconnectedness of these mathematical representations.
Frequently Asked Questions (FAQs)
Q: Is 73.33% the exact percentage equivalent of 11/15?
A: No, 73.33% is an approximation. The decimal representation of 11/15 is a repeating decimal (0.73333...). The exact percentage would be expressed as 73.333...%, with the "3" repeating infinitely. However, for practical purposes, rounding to two decimal places (73.33%) is sufficient.
Q: Can I use a different method to convert 11/15 to a percentage?
A: Yes, you can use various methods, such as long division, setting up proportions, or using online calculators. The choice depends on your preference and the tools available.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions and make decisions based on relative values. They are used extensively in various fields, including business, finance, science, and everyday life.
Q: What if the fraction involves larger numbers?
A: The same methods apply even with larger numbers. You can use a calculator or long division to efficiently convert the fraction to a percentage. The process remains consistent.
Q: How can I improve my skills in percentage calculations?
A: Practice is key. Work through various examples, try different methods, and solve problems related to real-world situations. Online resources and educational materials can provide additional practice exercises and explanations.
Conclusion
Converting 11/15 to a percentage is a straightforward process with multiple approaches. Understanding this conversion, along with the underlying concepts of fractions and percentages, is crucial for navigating numerous aspects of daily life and various academic and professional fields. By mastering this fundamental skill, you enhance your mathematical literacy and improve your ability to interpret and analyze data effectively. Remember that while 73.33% is a practical approximation, it’s important to understand the underlying mathematical principles and the limitations of rounding in specific contexts. Further exploration of percentage-related concepts will solidify your understanding and allow you to apply these skills to a wide range of situations.
Latest Posts
Latest Posts
-
Once And The Future King
Sep 20, 2025
-
Why Was High Heels Invented
Sep 20, 2025
-
Too Late Or To Late
Sep 20, 2025
-
Quotes From Ophelia In Hamlet
Sep 20, 2025
-
Cognitive Changes In Middle Adulthood
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 11 15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.