1 Percent Of 1 Million
marihuanalabs
Sep 03, 2025 · 5 min read
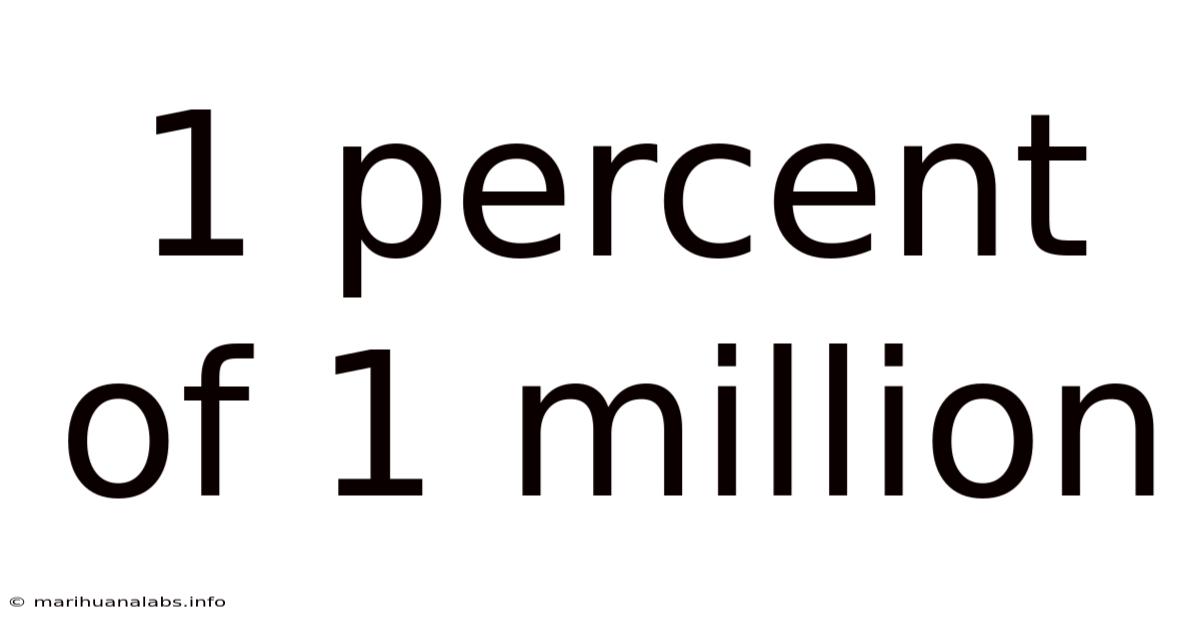
Table of Contents
Decoding 1% of 1 Million: A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending financial reports and statistical data. This article will delve into the seemingly simple calculation of "1% of 1 million," explaining not only the answer but also the underlying concepts, practical applications, and common misconceptions surrounding percentages. We'll explore the mathematical process, illustrate it with real-world examples, and even touch upon the broader implications of understanding proportional relationships.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 1% means 1 out of 100, or 1/100, which is equivalent to the decimal 0.01. This foundational understanding is key to accurately calculating percentages of any number.
Calculating 1% of 1 Million: The Math
Calculating 1% of 1 million is straightforward using the following methods:
-
Method 1: Direct Calculation
The most direct approach involves multiplying 1 million by the decimal equivalent of 1%, which is 0.01:
1,000,000 * 0.01 = 10,000
Therefore, 1% of 1 million is 10,000.
-
Method 2: Fraction Method
We can also express 1% as a fraction (1/100) and solve the equation:
(1/100) * 1,000,000 = 10,000
Again, the result is 10,000.
-
Method 3: Percentage as a Multiplier
Alternatively, consider that "percent" means "per hundred". This means 1% is 1 part out of 100 parts. Dividing 1,000,000 by 100 gives us 10,000, which is one hundredth of 1 million.
Regardless of the chosen method, the answer remains consistent: 1% of 1 million equals 10,000. This seemingly simple calculation has far-reaching implications in various fields.
Real-World Applications: Beyond the Textbook
The calculation of 1% of 1 million transcends the realm of abstract mathematics and finds practical application in numerous real-world scenarios:
-
Finance and Investments: Imagine an investment portfolio worth $1 million. A 1% increase in value would represent a gain of $10,000. Conversely, a 1% decrease would mean a loss of $10,000. Understanding this is crucial for assessing investment performance and managing risk. This concept extends to interest calculations, where a 1% annual interest on a $1 million loan or deposit would amount to $10,000 per year.
-
Sales and Marketing: In the business world, understanding percentages is vital for analyzing sales figures, market share, and campaign effectiveness. For a company with $1 million in annual revenue, a 1% increase in sales represents an additional $10,000 in revenue. This can inform strategic decisions regarding marketing investments and resource allocation. Analyzing market share similarly relies on understanding percentages and their implications for growth and competitiveness.
-
Population Statistics and Demographics: Government agencies and research organizations use percentages extensively to analyze population data. If a city has a population of 1 million, a 1% increase would represent an additional 10,000 residents. This kind of analysis is crucial for urban planning, infrastructure development, and resource management.
-
Scientific Research and Data Analysis: In scientific research, data analysis often involves calculating percentages to represent proportions and relationships within datasets. Whether analyzing survey results, experimental outcomes, or epidemiological data, percentages offer a standardized way to interpret and communicate findings. A 1% change in a statistically significant parameter could hold substantial implications.
-
Taxation and Government Revenue: Governments rely on taxes to generate revenue. A 1% tax on a $1 million property would generate $10,000 in tax revenue. Understanding these percentages is essential for policymakers in making fiscal decisions and managing public funds.
These examples highlight the widespread utility of understanding percentages, even in seemingly basic calculations like 1% of 1 million.
Misconceptions and Common Errors
Despite the apparent simplicity of percentage calculations, several common misconceptions can lead to errors:
-
Confusing Percentage Points and Percentages: A change from 5% to 6% is a one percentage point increase, not a 1% increase. A 1% increase from 5% would be 5.05%. This distinction is crucial in financial reporting and interpreting statistical data.
-
Incorrect Decimal Conversion: Failing to correctly convert percentages to decimals (e.g., mistaking 1% for 0.1 instead of 0.01) is a common mistake leading to inaccurate results.
-
Applying Percentages to Incorrect Bases: Ensuring you're applying the percentage to the correct base value is crucial. If calculating a discount on a marked-down price, ensure you apply the percentage to the original price, not the already reduced price.
-
Ignoring Context: The interpretation of percentages is highly context-dependent. A 1% increase in a small quantity might be insignificant, whereas a 1% increase in a large quantity could be substantial. Always consider the magnitude of the base value.
Addressing these misconceptions is key to ensuring accurate and meaningful interpretations of percentage calculations.
Expanding the Concept: Proportional Relationships
The calculation of 1% of 1 million illustrates a fundamental principle of proportional relationships. A percentage represents a proportion, a ratio comparing one part to a whole. Understanding proportions is crucial for scaling quantities, adjusting recipes, and solving various problems in math, science, and everyday life. This concept extends beyond simple percentages, encompassing more complex ratios and proportional reasoning skills.
Beyond 1%: Exploring Different Percentages of 1 Million
Let's extend the concept beyond just 1%:
-
10% of 1 million: This is simply 10 times the value of 1%, so 10 * 10,000 = 100,000.
-
25% of 1 million: This is equivalent to one-quarter of 1 million, so 1,000,000 / 4 = 250,000.
-
50% of 1 million: This is one-half of 1 million, so 1,000,000 / 2 = 500,000.
-
75% of 1 million: This is three-quarters of 1 million, so (3/4) * 1,000,000 = 750,000.
These calculations showcase the versatility of percentage calculations and their adaptability to various situations.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a crucial life skill with wide-ranging applications across multiple disciplines. The seemingly simple calculation of 1% of 1 million—equaling 10,000—serves as a springboard to explore more complex percentage calculations, proportional reasoning, and their practical implications in various real-world scenarios. By mastering these concepts and avoiding common pitfalls, individuals equip themselves with a powerful tool for effective decision-making and problem-solving in both professional and personal aspects of life. The ability to accurately interpret and apply percentages not only enhances numerical literacy but also fosters a deeper understanding of data analysis, financial management, and many other areas. So next time you encounter a percentage problem, remember the fundamentals and apply them with confidence.
Latest Posts
Latest Posts
-
I Miss You In German
Sep 05, 2025
-
Goddess Of Mercy Kuan Yin
Sep 05, 2025
-
Leslie Burke Bridge To Terabithia
Sep 05, 2025
-
52 Weeks Ago From Today
Sep 05, 2025
-
The Alchemist Of Paulo Coelho
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 1 Percent Of 1 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.