1 Divided By 1 9
marihuanalabs
Sep 19, 2025 · 5 min read
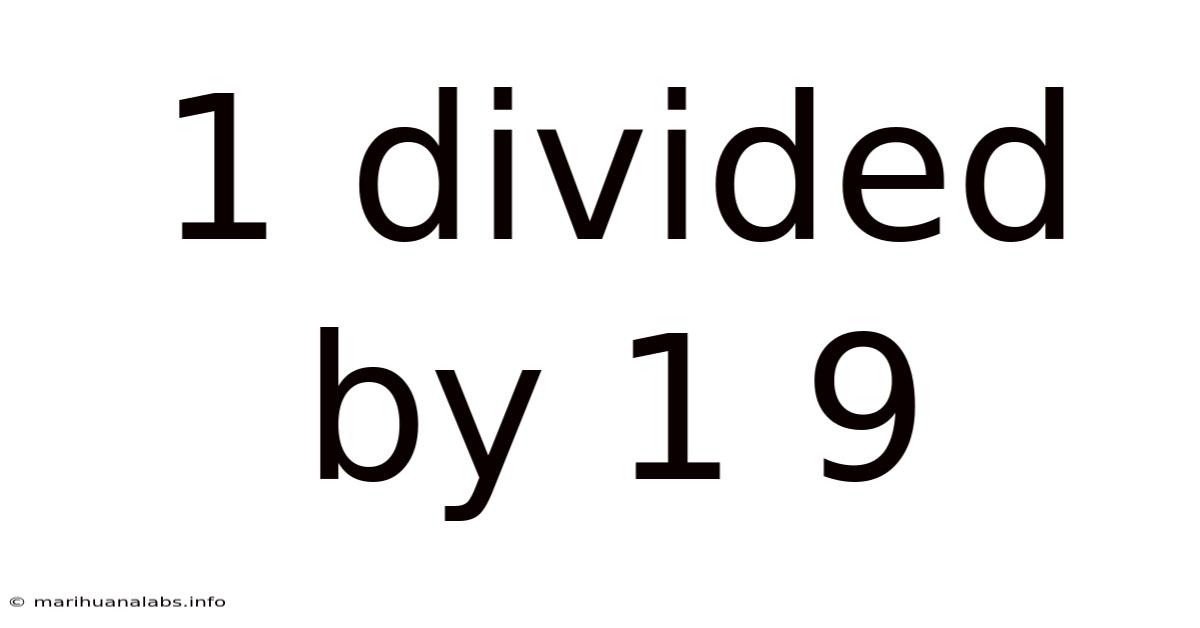
Table of Contents
Unraveling the Mystery: 1 Divided by 1.9 (and Understanding Decimal Division)
Have you ever encountered a division problem like 1 divided by 1.9 and found yourself scratching your head? This seemingly simple calculation can actually reveal a lot about decimal division and the underlying principles of mathematics. This article will explore this specific problem in detail, providing a step-by-step guide to solving it manually, explaining the underlying mathematical concepts, and addressing frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of how decimal division works. Understanding this seemingly simple calculation opens doors to more complex mathematical concepts.
Understanding the Problem: 1 ÷ 1.9
The problem, 1 ÷ 1.9, asks: "How many times does 1.9 fit into 1?" Since 1.9 is larger than 1, the answer will be less than 1, a decimal value. This is a crucial concept to grasp before diving into the solution. We're not looking for a whole number answer; instead, we're looking for a portion of 1.9 that fits into the whole number 1. This is where our understanding of decimals becomes vital.
Method 1: Long Division – A Step-by-Step Approach
The most straightforward method for solving 1 ÷ 1.9 is using long division. While calculators provide instant answers, understanding the manual process is key to grasping the underlying mathematical logic. Here's how to perform long division for this problem:
-
Set up the problem: Write the division problem as 1 ÷ 1.9 or, more conventionally for long division, 1.0 ÷ 1.9. We added a zero after the decimal point in the dividend (1) to help us with the division process.
-
Adjust for decimals: To make the divisor (1.9) a whole number, we multiply both the divisor and the dividend by 10. This does not change the result because we are essentially multiplying the fraction by 1 (10/10 = 1). This gives us 10 ÷ 19.
-
Begin the long division: Now, perform long division as you would with whole numbers.
0.5263... 19 | 10.0000 9.5 --- 0.50 0.38 ---- 0.120 0.114 ---- 0.0060 0.0057 ---- 0.0003 -
Interpret the result: The long division reveals that 1 ÷ 1.9 ≈ 0.5263. The three dots (...) indicate that the decimal continues infinitely. This is a repeating decimal, meaning the digits will repeat in a pattern, but it’s not a simple, easily discernible repetition like 1/3 = 0.333...
-
Rounding: For practical purposes, we often round the answer to a specific number of decimal places. For example, rounded to three decimal places, the answer is 0.526. The level of precision required depends on the context of the problem.
Method 2: Converting to Fractions – An Alternative Approach
Another way to approach this problem is by converting the decimal 1.9 into a fraction and then performing the division.
-
Convert 1.9 to a fraction: 1.9 can be written as 19/10.
-
Rewrite the division: The problem now becomes 1 ÷ (19/10).
-
Invert and multiply: To divide by a fraction, we invert the second fraction (reciprocal) and multiply. This gives us 1 x (10/19) = 10/19.
-
Convert to decimal: Now, divide 10 by 19 using long division (as shown in Method 1), or use a calculator to obtain the decimal approximation: 10/19 ≈ 0.5263.
This fractional method confirms the result obtained through long division, demonstrating the equivalence of the two approaches. The fractional method often offers a more elegant and conceptually clear path, particularly when dealing with more complex decimal divisions.
The Mathematical Concept: Decimal Division and its Implications
The process of dividing by a decimal involves several key mathematical concepts. Understanding these deepens our appreciation of the seemingly simple calculation:
-
Decimal Representation: Decimal numbers represent fractions where the denominator is a power of 10 (10, 100, 1000, etc.). This system allows for a consistent and efficient representation of numbers between integers.
-
Equivalent Fractions: Multiplying both the numerator and denominator of a fraction by the same number doesn't change its value. We used this principle to eliminate the decimal in the divisor, making the long division simpler.
-
Reciprocal: The reciprocal of a number is 1 divided by that number. In the fraction method, we used the reciprocal to convert division into multiplication, a simpler operation.
-
Repeating Decimals: Many fractions, when converted to decimals, result in infinitely repeating sequences of digits. This highlights the inherent limitations of representing some rational numbers (fractions) exactly using a finite decimal representation.
-
Approximation and Rounding: Since repeating decimals cannot be written exactly, we often need to round them to a certain number of decimal places based on the desired level of accuracy. The context of the problem determines the appropriate level of rounding.
Frequently Asked Questions (FAQ)
-
Q: Why is the result a decimal less than 1? A: Because we're dividing a smaller number (1) by a larger number (1.9). The result represents a fraction of 1.9 that fits within 1.
-
Q: Is there a way to avoid long division? A: Yes, a calculator provides the quickest solution. The long division method is primarily for educational purposes, showing the underlying process. The fraction method also avoids extensive long division.
-
Q: What if the dividend was larger than the divisor (e.g., 1.9 ÷ 1)? A: In that case, the result would be greater than 1. The division would proceed similarly but would yield a whole number part and possibly a decimal part.
-
Q: How important is understanding the long division method? A: While calculators are readily available, understanding long division provides a deeper appreciation of the arithmetic process and helps in troubleshooting errors or understanding more complex calculations.
Conclusion: Beyond the Simple Calculation
While the initial question, 1 divided by 1.9, seems basic, exploring its solution unveils a wealth of information about decimal division, fractions, and the fascinating world of numerical representation. From long division to the use of reciprocals and the understanding of repeating decimals, this seemingly simple problem serves as a gateway to more advanced mathematical concepts. Mastering these fundamental concepts strengthens your mathematical foundation and enhances your problem-solving skills in various contexts. Remember, it's not just about getting the answer (approximately 0.5263); it’s about understanding the why behind the answer. This deeper understanding is what truly empowers your mathematical journey.
Latest Posts
Latest Posts
-
Why Is Verbal Communication Important
Sep 19, 2025
-
Heavy Looking Rather Portentous Man
Sep 19, 2025
-
Dividing By 10 And 100
Sep 19, 2025
-
Words That Rhyme With Mirror
Sep 19, 2025
-
75 Days From 1st Jan
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.