1 3 Divided By 4
marihuanalabs
Sep 13, 2025 · 6 min read
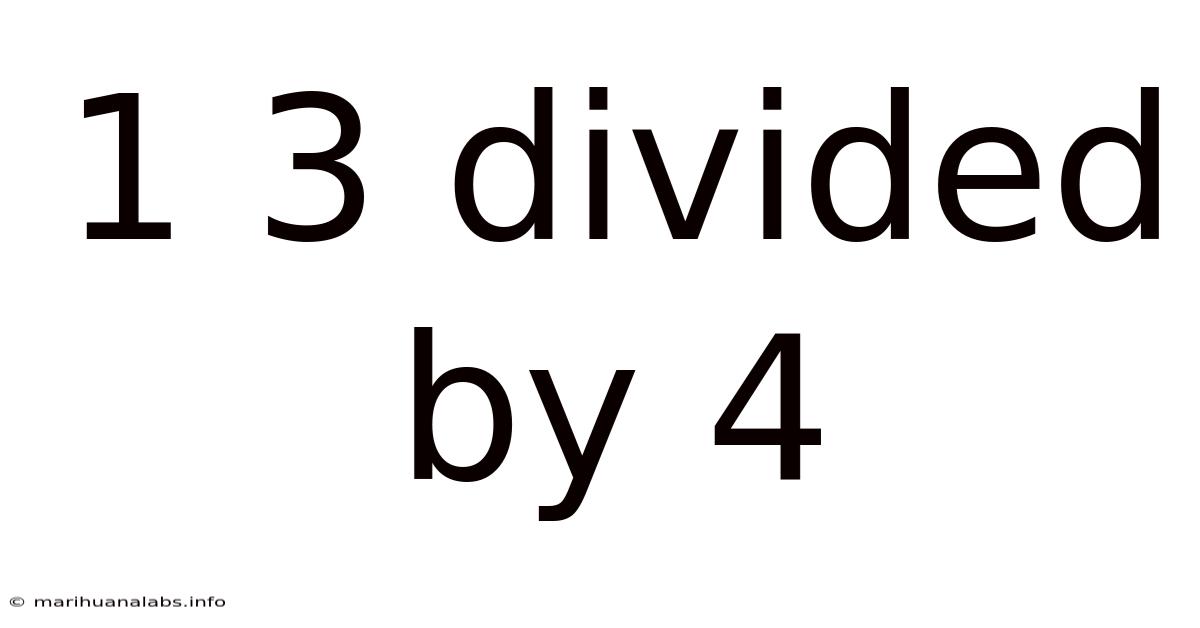
Table of Contents
Unpacking 1 3/4: A Deep Dive into Fractions and Mixed Numbers
Understanding fractions, especially mixed numbers like 1 3/4, is fundamental to grasping mathematical concepts. This seemingly simple fraction holds a world of mathematical principles and practical applications. This article will delve into the intricacies of 1 3/4, exploring its representation, conversions, operations, and real-world examples. We'll demystify this fraction, empowering you to confidently tackle similar problems and build a stronger foundation in mathematics.
Introduction: What is 1 3/4?
1 3/4 is a mixed number. A mixed number combines a whole number (1 in this case) and a proper fraction (3/4). It represents a quantity greater than one but less than two. Understanding mixed numbers is crucial for various applications, from baking (measuring ingredients) to calculating distances and proportions. This seemingly simple fraction provides a perfect entry point to understanding more complex fractional operations.
Different Representations of 1 3/4
1 3/4 can be expressed in several ways, each with its own utility:
-
Mixed Number: This is the most common representation: 1 3/4. It clearly shows the whole number and fractional parts.
-
Improper Fraction: An improper fraction has a numerator larger than or equal to its denominator. To convert 1 3/4 to an improper fraction, we multiply the whole number (1) by the denominator (4), add the numerator (3), and keep the same denominator: (1 * 4) + 3 = 7. Therefore, 1 3/4 is equivalent to 7/4. Improper fractions are often more convenient for calculations.
-
Decimal: Fractions can be expressed as decimals by performing the division indicated by the fraction. Dividing 7 by 4 (from the improper fraction) gives us 1.75. Decimals are useful for calculations involving other decimal numbers and for displaying values in certain contexts.
-
Percentage: To express 1 3/4 as a percentage, we convert it to a decimal (1.75) and multiply by 100%: 1.75 * 100% = 175%. Percentages are particularly useful for representing proportions and changes.
Working with 1 3/4: Mathematical Operations
Understanding how to perform various mathematical operations with 1 3/4 is critical. Let's explore addition, subtraction, multiplication, and division:
Addition:
Adding 1 3/4 to another number depends on the format of the other number. If adding another mixed number, it's often easiest to convert both to improper fractions first. For example, adding 1 3/4 to 2 1/2:
- Convert to improper fractions: 1 3/4 = 7/4 and 2 1/2 = 5/2.
- Find a common denominator: The least common multiple of 4 and 2 is 4.
- Rewrite the fractions with the common denominator: 7/4 and 10/4.
- Add the numerators: 7/4 + 10/4 = 17/4.
- Convert back to a mixed number (if desired): 17/4 = 4 1/4.
Therefore, 1 3/4 + 2 1/2 = 4 1/4.
If adding a whole number, simply add the whole numbers together and keep the fraction: 1 3/4 + 3 = 4 3/4. Adding a decimal would involve converting 1 3/4 to a decimal (1.75) and performing decimal addition.
Subtraction:
Subtraction follows a similar process. Let's subtract 1 1/4 from 1 3/4:
- Convert to improper fractions: 1 3/4 = 7/4 and 1 1/4 = 5/4.
- Subtract the numerators: 7/4 - 5/4 = 2/4.
- Simplify the fraction: 2/4 = 1/2.
Therefore, 1 3/4 - 1 1/4 = 1/2.
Multiplication:
Multiplying 1 3/4 by another number also benefits from converting to an improper fraction:
Let's multiply 1 3/4 by 2:
- Convert 1 3/4 to an improper fraction: 7/4.
- Multiply: (7/4) * 2 = 14/4.
- Simplify: 14/4 = 7/2 = 3 1/2.
Therefore, 1 3/4 * 2 = 3 1/2.
Division:
Dividing with fractions involves inverting (reciprocating) the second fraction and multiplying. Let's divide 1 3/4 by 1/2:
- Convert 1 3/4 to an improper fraction: 7/4.
- Invert the second fraction: 1/2 becomes 2/1.
- Multiply: (7/4) * (2/1) = 14/4.
- Simplify: 14/4 = 7/2 = 3 1/2.
Therefore, 1 3/4 / (1/2) = 3 1/2.
Real-World Applications of 1 3/4
The seemingly simple fraction 1 3/4 appears in countless real-world situations:
-
Cooking & Baking: Recipes frequently call for 1 3/4 cups of flour, 1 3/4 teaspoons of baking powder, or other quantities.
-
Measurements: Calculating distances, lengths, or volumes often involves fractions like 1 3/4 inches, 1 3/4 meters, or 1 3/4 liters.
-
Time: 1 3/4 hours represents 1 hour and 45 minutes.
-
Finance: Calculating discounts, profits, or interest rates can involve this fraction.
-
Construction: Measurements in construction projects frequently utilize fractions.
Frequently Asked Questions (FAQ)
Q: How do I convert 1 3/4 to a percentage?
A: Convert 1 3/4 to a decimal (1.75) then multiply by 100%: 1.75 * 100% = 175%.
Q: What is the simplest form of 1 3/4?
A: While 1 3/4 is already in a commonly used form, the improper fraction equivalent 7/4 could be considered a simpler form in the context of some mathematical operations. However, 1 3/4 is perfectly acceptable and often preferred for clarity.
Q: Can 1 3/4 be expressed as a ratio?
A: Yes. The ratio representation of 1 3/4 is 7:4. This shows the relationship between the total parts (7) and the denominator (4).
Q: How do I compare 1 3/4 to other fractions?
A: Convert all fractions to either improper fractions or decimals for easy comparison. For instance, to compare 1 3/4 to 5/3, convert them to improper fractions (7/4 and 5/3) then find a common denominator (12) to compare 21/12 and 20/12. Therefore, 1 3/4 (21/12) is greater than 5/3 (20/12).
Conclusion: Mastering Fractions
Understanding fractions, including mixed numbers like 1 3/4, is essential for mathematical proficiency and navigating everyday life. This article has explored the multiple representations of 1 3/4, delved into various mathematical operations involving this fraction, and highlighted its numerous real-world applications. By mastering these concepts, you'll enhance your mathematical skills and develop a stronger grasp of numerical relationships. Remember that consistent practice and a curious approach are key to building confidence and fluency in working with fractions. Don't hesitate to explore further examples and challenges to solidify your understanding. The more you work with fractions, the more intuitive they will become.
Latest Posts
Latest Posts
-
A University Or An University
Sep 13, 2025
-
Cast Of Julius Caesar 2002
Sep 13, 2025
-
Gross Motor Function Classification System
Sep 13, 2025
-
Pan American Highway Route Map
Sep 13, 2025
-
How Many Inches Is 23cm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.