1 1 X 1 1
marihuanalabs
Sep 15, 2025 · 5 min read
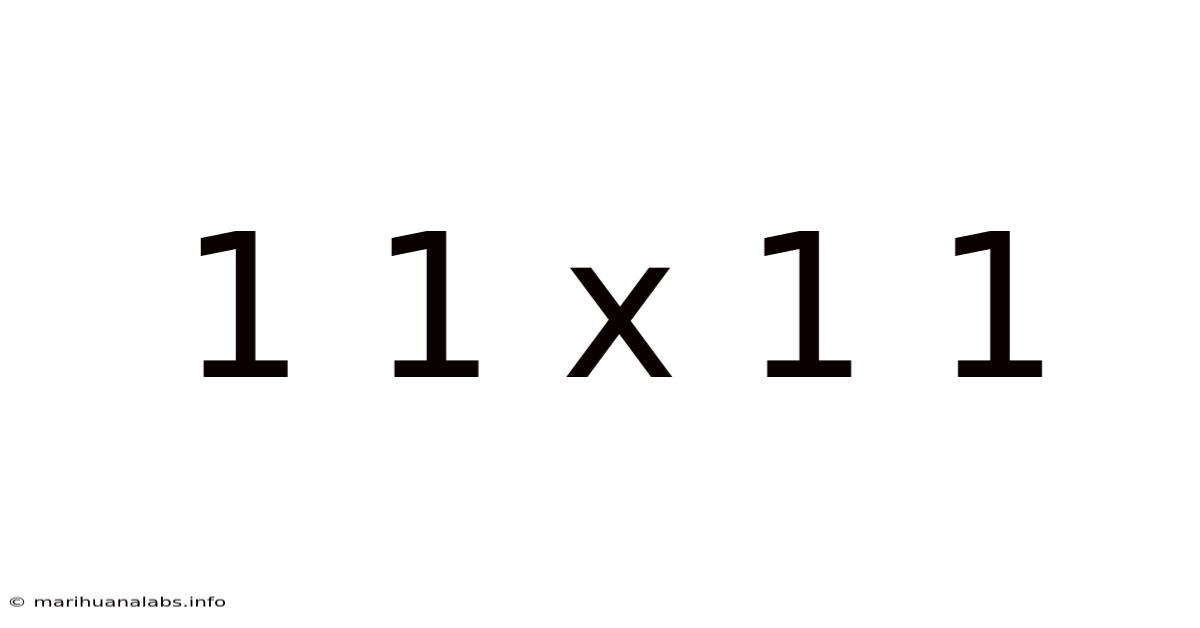
Table of Contents
Decoding 11 x 11: A Deep Dive into Multiplication, Patterns, and Beyond
The seemingly simple multiplication problem, 11 x 11, serves as a gateway to exploring fascinating mathematical concepts. While the answer, 121, is easily obtained through basic multiplication, a deeper examination reveals underlying patterns, connections to other mathematical areas, and even applications in more advanced fields. This article will dissect this seemingly simple problem, unraveling its complexities and demonstrating its surprising depth. We'll explore the mechanics of multiplication, examine the unique properties of the number 121, delve into related mathematical sequences and patterns, and discuss its relevance beyond basic arithmetic.
Understanding the Fundamentals: The Mechanics of 11 x 11
At its core, 11 x 11 represents repeated addition. It means adding eleven eleven times: 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11. This approach, while functional, is time-consuming for larger numbers. The standard multiplication algorithm provides a more efficient method.
We can break down the multiplication using the distributive property:
11 x 11 = (10 + 1) x (10 + 1) = 10 x (10 + 1) + 1 x (10 + 1) = 100 + 10 + 10 + 1 = 121
This method showcases the underlying structure of multiplication and demonstrates how it works with numbers composed of tens and units. It's a foundational concept that helps build understanding for more complex multiplications.
The Uniqueness of 121: Exploring its Properties
The product of 11 x 11, 121, possesses several unique properties:
-
Perfect Square: 121 is a perfect square, meaning it's the result of squaring a whole number (11² = 121). Perfect squares are fundamental in algebra and geometry, appearing frequently in various mathematical contexts.
-
Palindromic Number: 121 is a palindrome, meaning it reads the same forwards and backward. Palindromes appear in various number systems and have intrigued mathematicians for centuries due to their inherent symmetry.
-
Sum of Consecutive Odd Numbers: 121 can be expressed as the sum of consecutive odd numbers: 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 = 121. This property connects it to the sum of arithmetic progressions.
-
Factorization: The prime factorization of 121 is 11 x 11, highlighting its nature as a perfect square. This simple factorization allows for easy calculations involving 121.
Patterns and Sequences: Unveiling Connections
The result of 11 x 11, and the process of multiplying numbers close to 10, leads to observing patterns that can simplify calculations and reveal underlying mathematical principles.
Consider the following multiplications:
- 11 x 11 = 121
- 11 x 12 = 132
- 11 x 13 = 143
- 11 x 14 = 154
- 11 x 15 = 165
Notice a pattern? The tens digit increases by one, while the units digit decreases by one. This pattern works up to 11 x 19, after which the pattern slightly modifies due to carrying over. Understanding these patterns allows for rapid mental calculations, showcasing the beauty and elegance of mathematical shortcuts.
Extending the Concept: Multiplying Larger Numbers
The principles applied to 11 x 11 can be extended to larger numbers. For example, multiplying two-digit numbers that are close to 100 can utilize similar strategies. Consider 98 x 97:
We can rewrite these as (100 - 2) x (100 - 3). Expanding this using the distributive property (FOIL method) will reveal the answer efficiently.
This showcases how the foundational understanding gained from analyzing 11 x 11 contributes to solving more complex problems. The application of the distributive property remains crucial in simplifying calculations.
Applications Beyond Basic Arithmetic
The simple multiplication 11 x 11, although appearing basic, touches upon concepts with broader applications:
-
Computer Science: Binary systems, crucial to computer operations, rely on the principles of multiplication and powers of 2. Understanding basic multiplication is fundamental to comprehending how computers perform calculations.
-
Algebra: The concept of perfect squares is vital in algebra, particularly when dealing with quadratic equations and their solutions. 121, being a perfect square, exemplifies these fundamental concepts.
-
Geometry: The area of a square with side length 11 is 121 square units. This simple geometric application connects arithmetic with spatial reasoning.
-
Number Theory: 121's properties as a perfect square and a palindrome connect it to broader areas of number theory that explore the fascinating properties and relationships within number systems.
Frequently Asked Questions (FAQ)
Q: Are there any shortcuts for multiplying by 11?
A: Yes, there are several mental math tricks for multiplying by 11. For two-digit numbers, you can add the digits and place the sum in between the original digits. For example, for 23 x 11, you add 2 and 3 (which is 5), and place the 5 between the 2 and 3 to get 253. This trick works for many two-digit numbers but requires adjustments for numbers where the sum of the digits is greater than 9.
Q: Is 121 a prime number?
A: No, 121 is not a prime number. A prime number is only divisible by 1 and itself. 121 is divisible by 11, making it a composite number.
Q: What are some real-world applications of understanding perfect squares?
A: Perfect squares have applications in various areas. In construction, calculating areas and volumes often involves perfect squares. In computer graphics, understanding squares and their properties is essential for creating and manipulating images. In physics, many formulas involve squares, such as calculating kinetic energy or gravitational force.
Conclusion: The Enduring Significance of 11 x 11
The seemingly simple problem of 11 x 11 serves as a powerful illustration of how fundamental mathematical concepts can lead to deeper insights and broader applications. From the basic mechanics of multiplication to the unique properties of 121, and its connections to patterns, sequences, and advanced mathematical fields, this problem showcases the inherent beauty and interconnectedness within mathematics. It encourages us to look beyond the immediate answer and explore the underlying principles, fostering a deeper appreciation for the elegance and power of mathematical thinking. By understanding the intricacies of 11 x 11, we gain a stronger foundation for tackling more complex problems and appreciating the interconnectedness of seemingly disparate mathematical concepts. The exploration of this seemingly simple equation unveils a world of mathematical richness, encouraging curiosity and a deeper understanding of the building blocks of mathematics.
Latest Posts
Latest Posts
-
Words With The Silent K
Sep 15, 2025
-
Wall Mount For Basketball Backboard
Sep 15, 2025
-
God Of Small Things Summary
Sep 15, 2025
-
Capital Of Oman Crossword Clue
Sep 15, 2025
-
Opaque Vs Translucent Vs Transparent
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 1 X 1 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.